One possible strategy for trading the financial markets is utilising reinforcement learning algorithms, and frame the
trading task as a "game", where the agent collects rewards for good trades and negative rewards for bad trades.
This particular personal project does a deep dive into common reinforcement learning strategies, before
applying them to the stock market.
Before diving straight into a trading environment, we will sanity check our implementation and tune the function approximator (neural network)
using the well known cartpole game provided by OpenAI Gym/Gymnasium (fig. 1). The code used in this project can be found
here.
Included in the repository is a full set of python unittests which check basic functionality of each of the implemented models to ensure
that the model is working as intended.

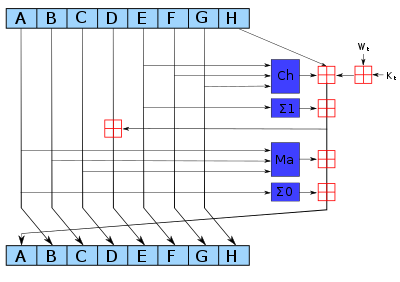
We will be utilizing the Q-learning algorithm (fig. 2), which is an off-policy algorithm (which means it chooses actions in
a different manner compared to the policy the agent is trying to learn) which uses a temporal difference TD(0) update.
When using a neural network to approximate the action-value function (usually denoted with Q(s,a)), the network is
commonly referred to as DQN. The DQN can be augmented in certain ways to produce other variants which can excel under
certain circumstances; namely Double DQN, DynaQ, DynaQ+ and even dueling DQNs (which will not be covered in this project).
We will be testing the efficacy of these models on the aforementioned environment, before eventually moving to predicting optimal trades.
The DQN itself is a very powerful model which was demonstrated to play many Atari games with good results and even achieving super human play
in some games. The Q-learning algorithm can be applied to both tabular and continuous environments, by estimating a value for each possible
action and state combo. The Q-learning update is mathematically proven to converge to the optimal policy under certain conditions; namely that
each state is visited an infinite number of times. However, as we can only train for finite time periods, sometimes the Q-learning agent
can get stuck in a local minima, and one commonly known issue is overestimation. In fact, when performing a deep dive on the DQN using a
basic toy environment which always remains in the same state, with two possible actions, 0 and 1 - where 1 always yields a reward of 1, whereas
the action zero permanently grants zero reward, I observed that the estimated value for action zero often gets overestimated during training, despite
the model never encountering a reward for that action; this is because of the greedy term which takes the maximum value of the value function for the
next state.
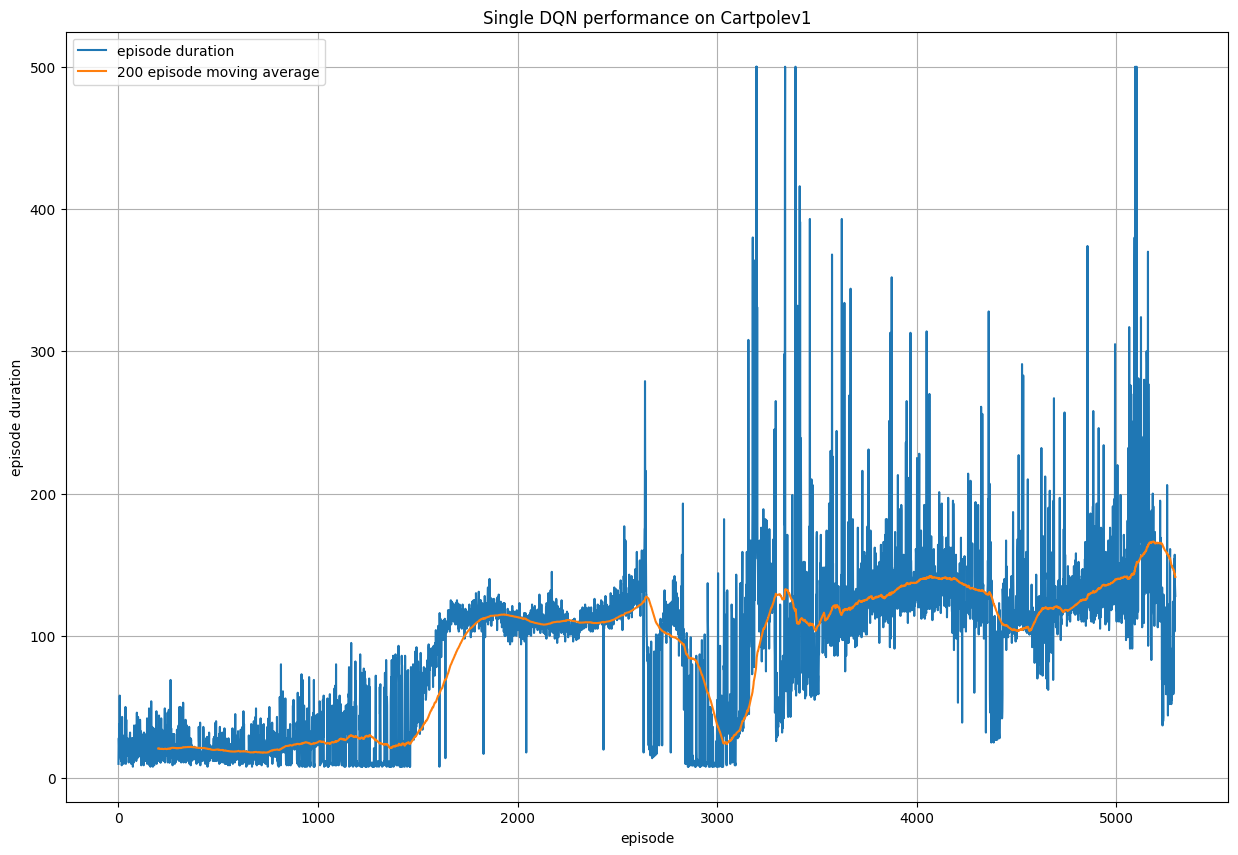
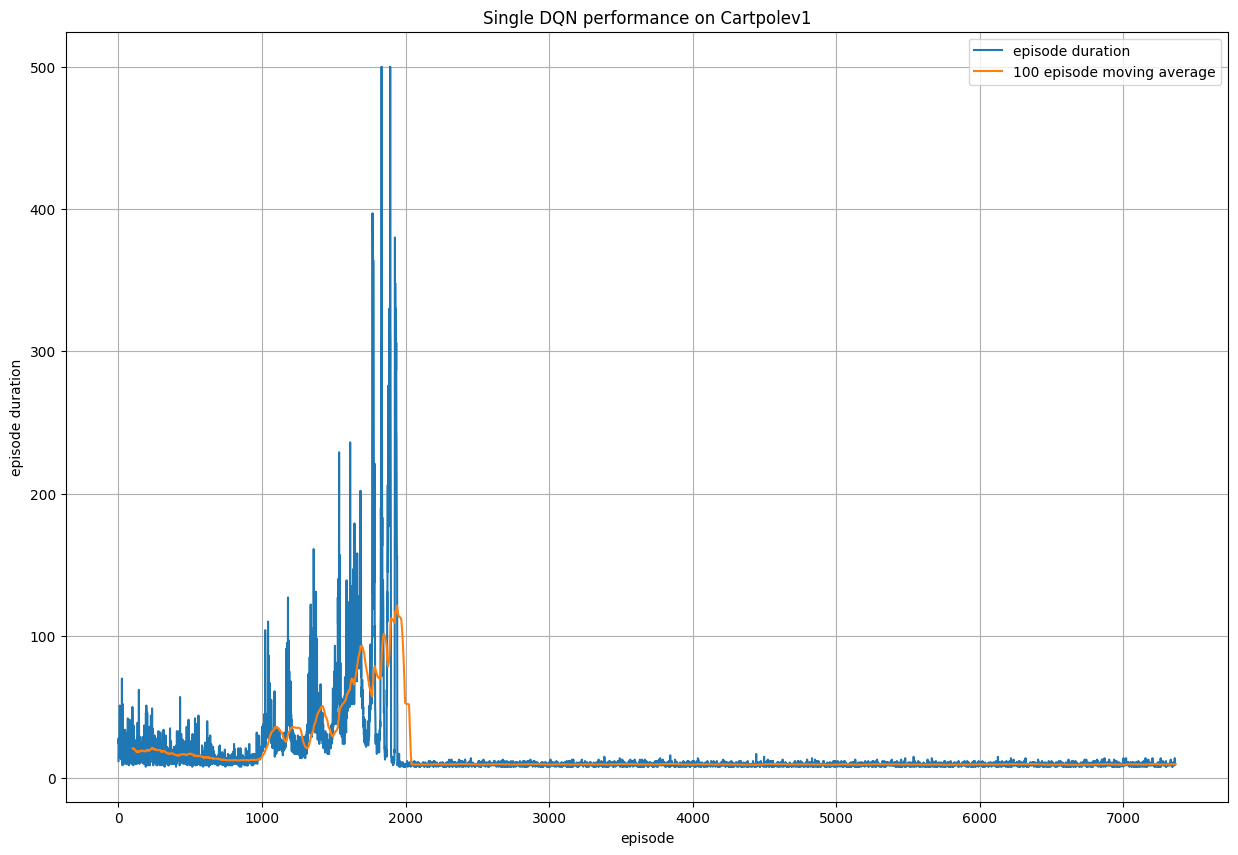
Here we show the reward versus time plots for the DQN itself, and it can be seen that the model is highly unstable and struggles to reach
the optimal policy, even after 5000 episodes of training.
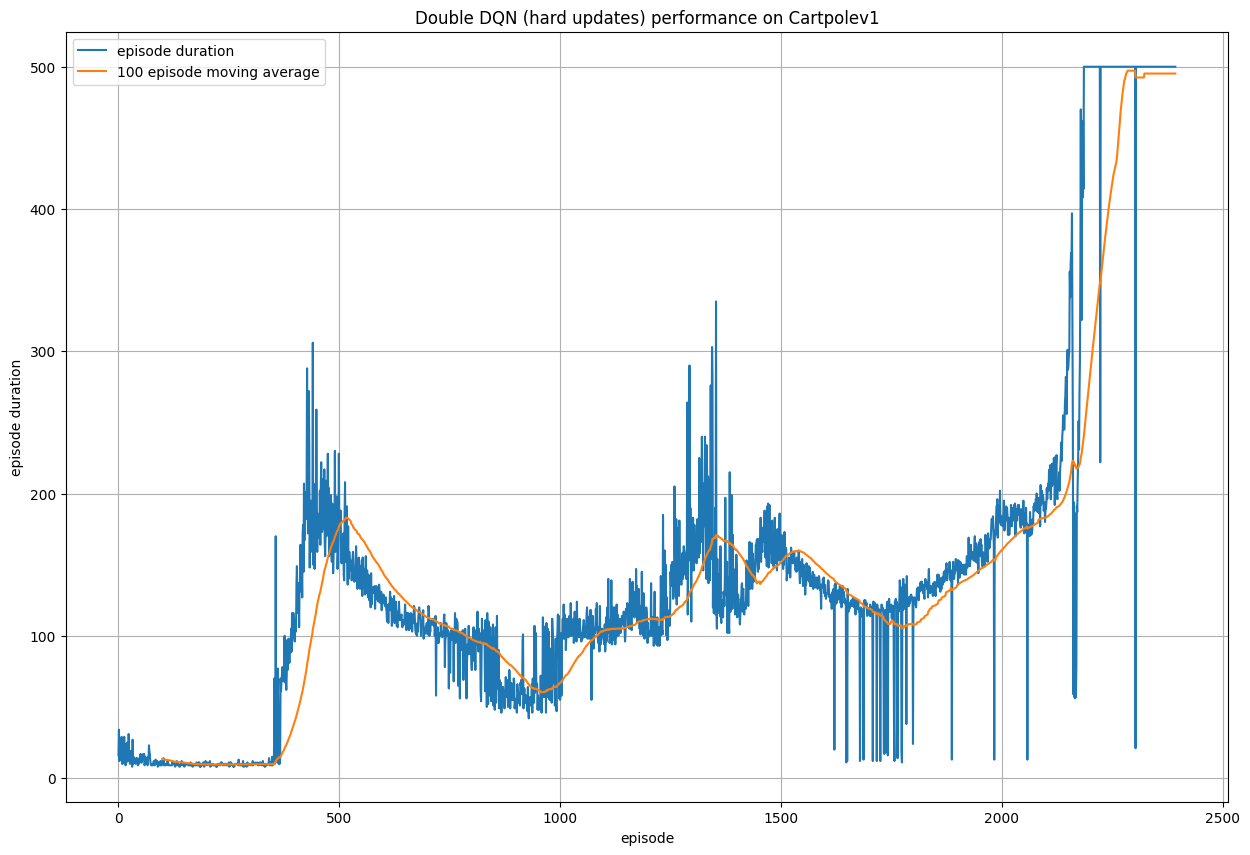
We can augment the DQN model such that we duplicate the Q-network to form a policy network and a target network. The intuition behind this construction is to mitigate the overestimation problem and the "moving target" problem. By fixing the one network and updating the other, we can fix the policy while updating which makes the training much more stable. Obviously the fixed network prediction will be bad initially, but it is updated periodically to match the network that is being updated. Additionally, we experiment with hard and soft updates, which are complete updates at intervals, or small interpolations at each time step.
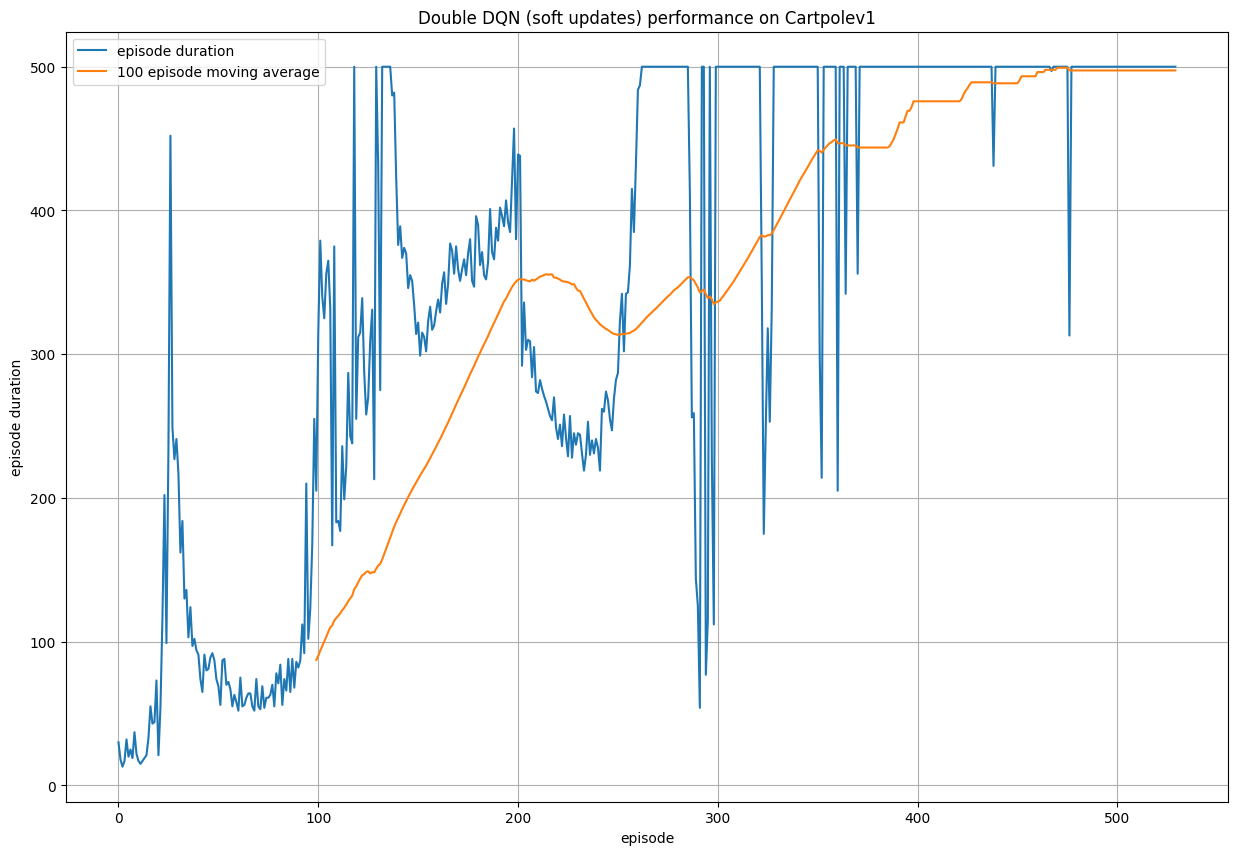
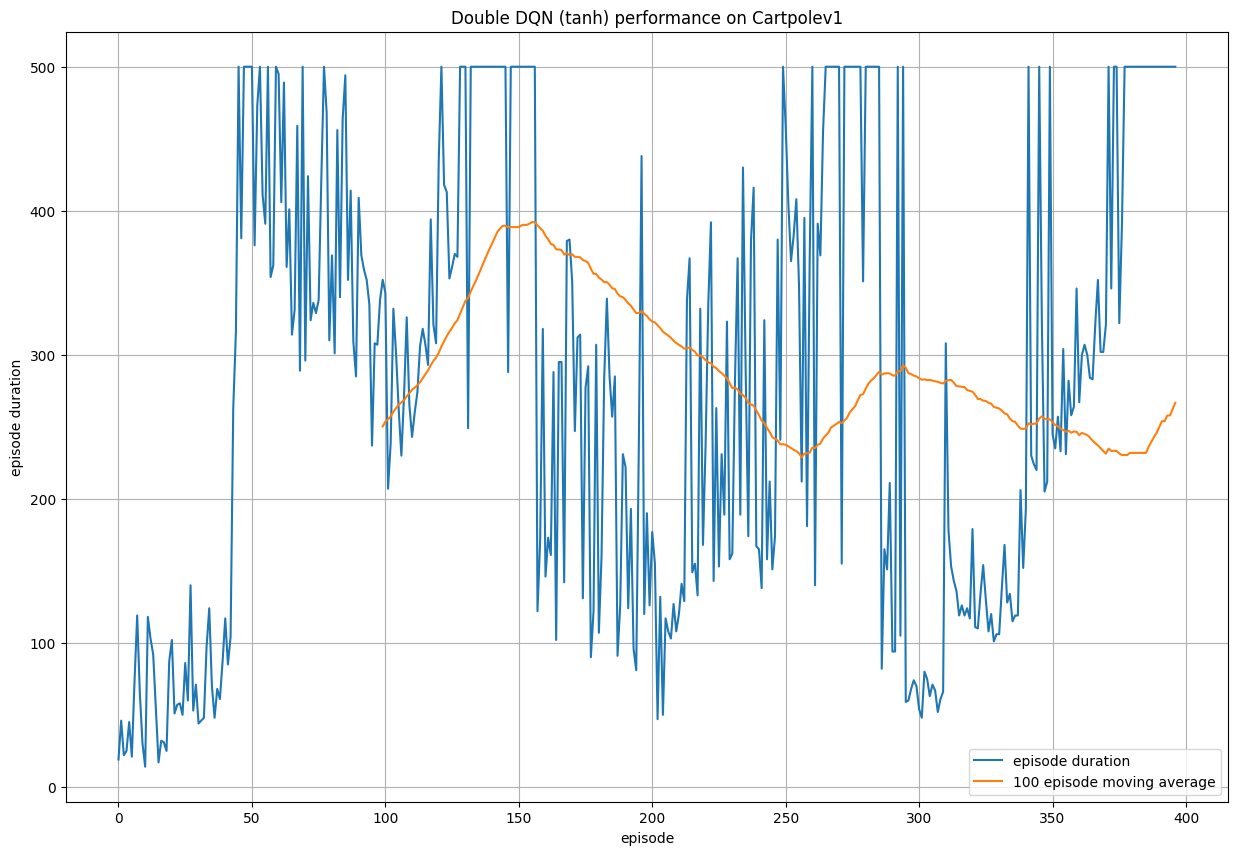
The performance of such agents also changes with different activation functions used within the neural network, and we experiment with ReLU (used in all experiments above), GeLU and Tanh. GeLU exhibits the strongest performance, being a stronger alternative to ReLU in most cases, due to preventing neurons from "dying out".
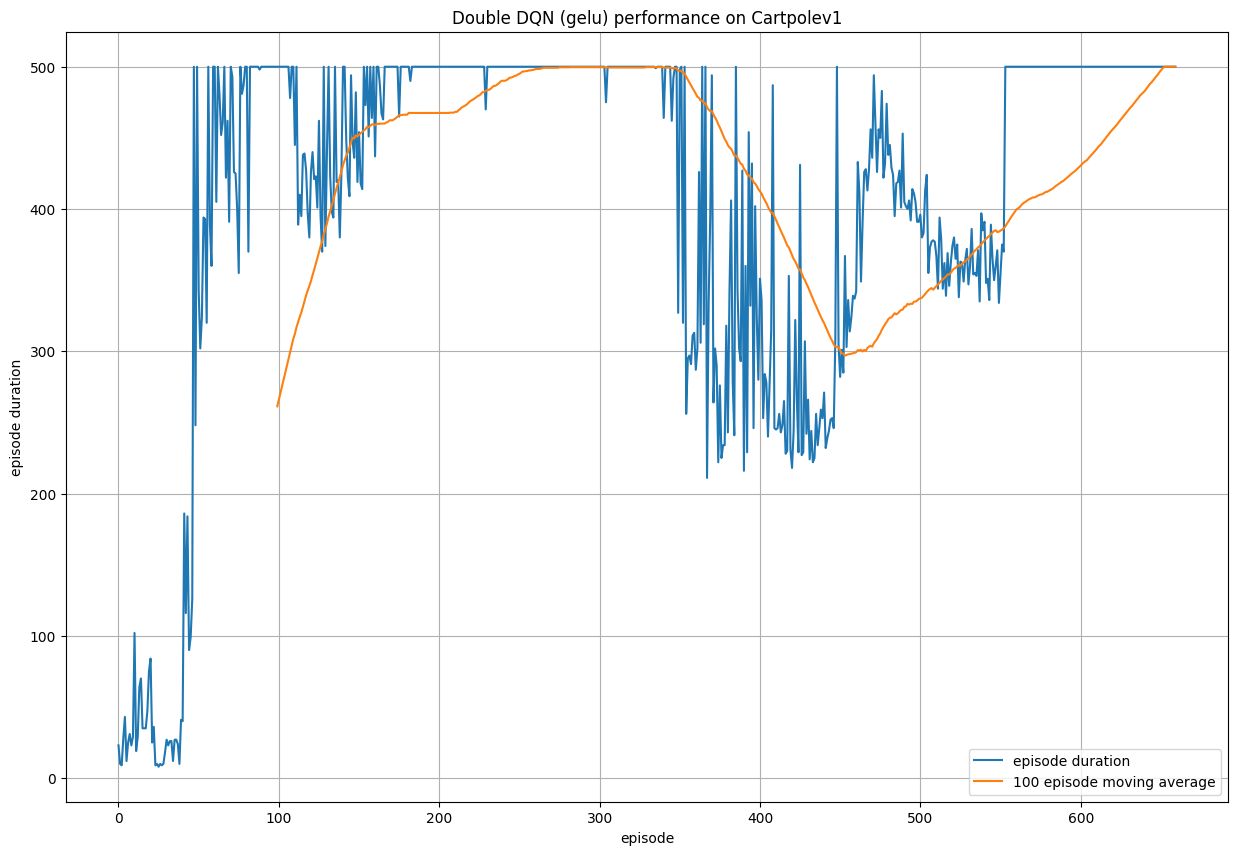
Finally, we test the performance of the DynaDQN algorithm. This is another augmentation of the DQN algorithm, where this time we
simultaneously build a model of the environment internally, which we can use to plan ahead. What this means is past observations are used
to train an internal world model which tries to learn - in this case - a mapping from (state, action) to next state, reward. By doing this, we
can condense our past knowledge into a model which can be used to generate additional fabricated observations which can be used to supplement
actual observations. Every training step that uses these generated observations are called planning steps, and in general, this allows the DynaDQN
to learn the optimal policy from fewer interactions with the environment. This can be useful when interactions with the world is costly. For the world
model we use a random forest regressor.

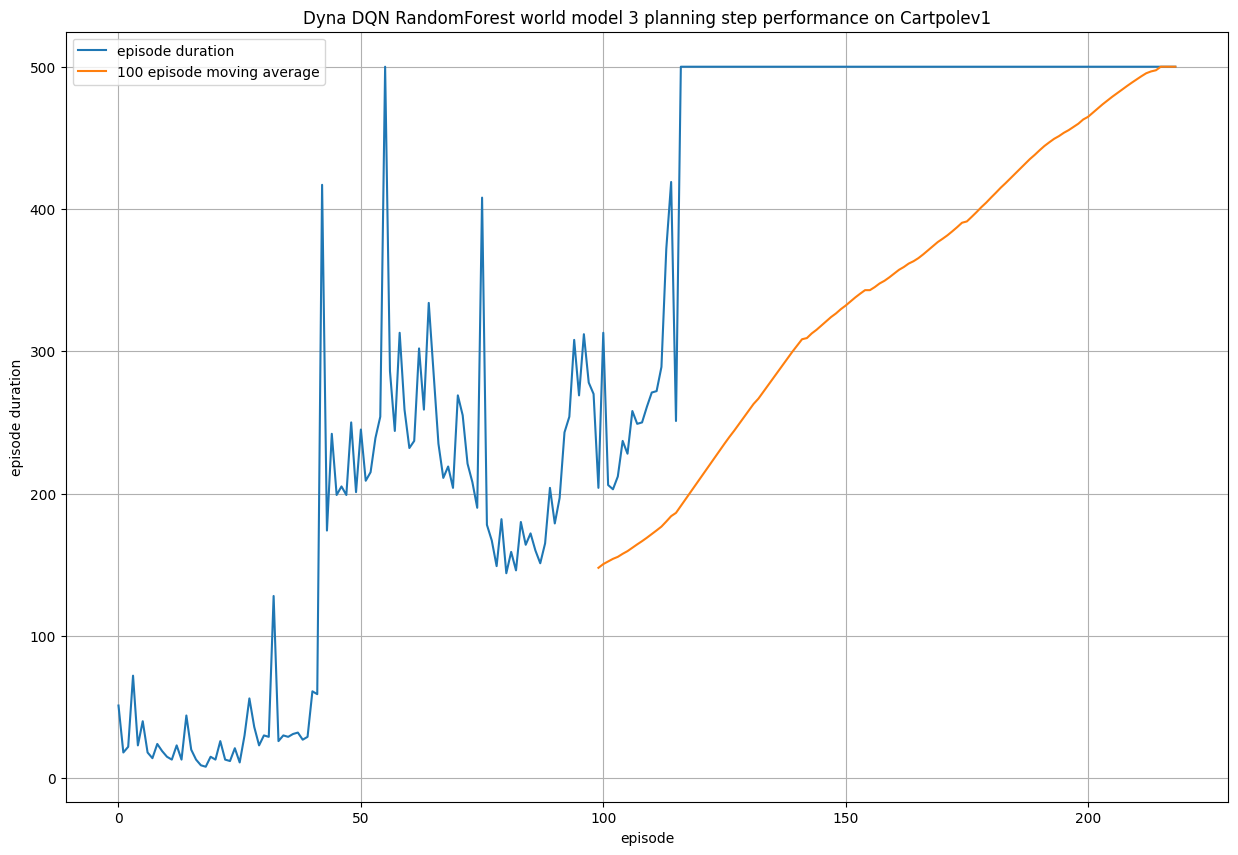
Using 3 planning steps for each actual observation, we can observe that the DynaDQN algorithm training appears more stable and converges to the
optimal policy in less episodes compared to all previous models. Note that the "quality" of such fabricated observations are lower than actual observations
(due to innaccuracies in the world model). So it is important to ensure that not too many planning steps are used.
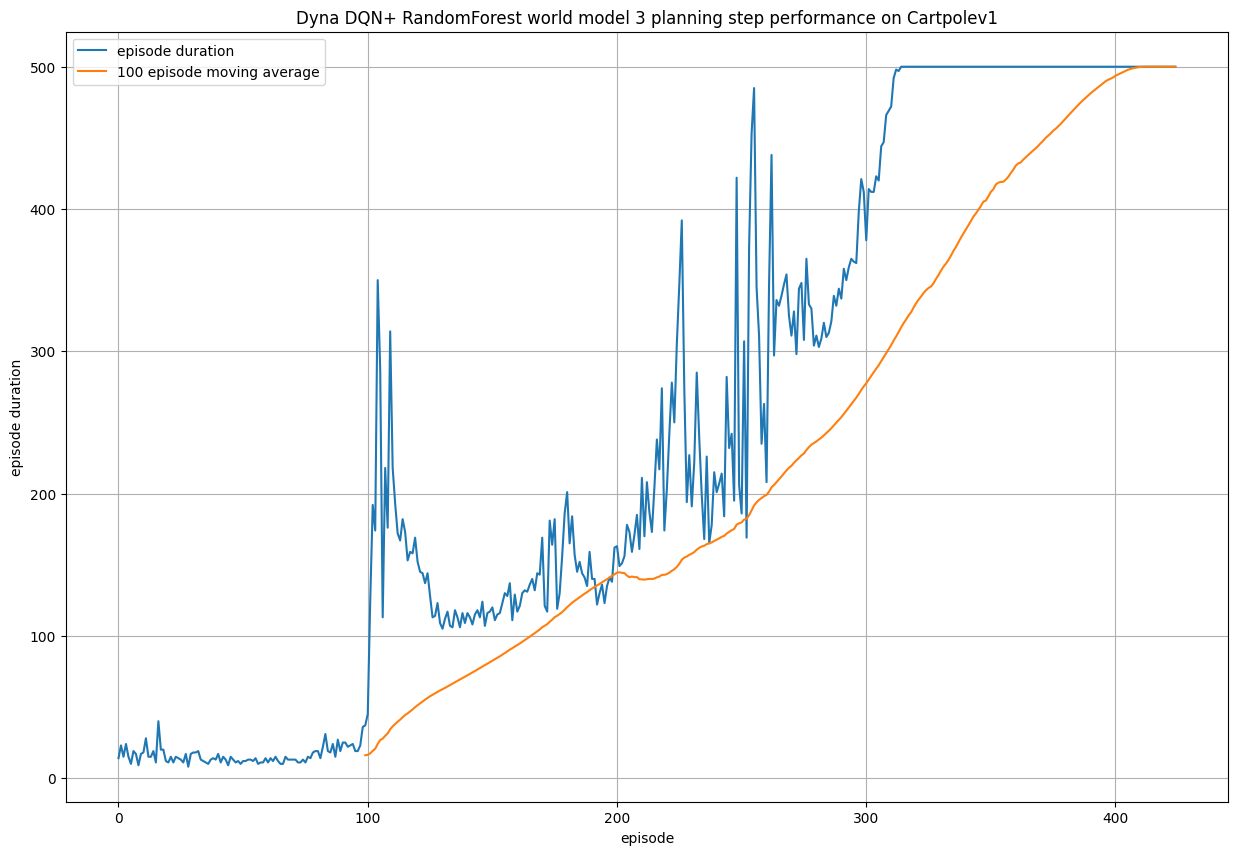
The last model I implemented is the Dyna Q+ algorithm, which records the last time an action was chosen in a particular state, and uses this to
encourage exploration over time of under trialled actions. This is especially powerful for changing environments as the algorithm is
more inclined to explore new actions if they haven't been used in a while. For this particular task, which uses a static environment, the extra exploration
provides no additional benefit. In fact, the extra exploration of potentially bad actions means that the algorithm takes more episodes to converge to the
optimal policy.
For Trading stocks, the DQN algorithm was trialled using the gym trading environment. We omit the discussion of any Dyna models in this section
as it is well known that modelling stock data is a difficult problem, let alone predicting how each of the individual features transition (modelling
state to state transitions).
These trading gym environments use the exact same methods as the regular
gym environments, but use a user defined dataframe which contains price information of a particular stock. For this task, the data is preprocessed to
include information on some of the most common financial indicators, such as simple moving averages, exponential moving averages, RSI and the MACD. These
are presented alongside price information to the agent, which returns either 1 for buy, 0 for neutral position and -1 for sell. Using the premade
gym environment makes it easy to train on multiple stocks. In this example we try training a DQN algorithm on AAPL, AMZN and GOOG stock prices for the last
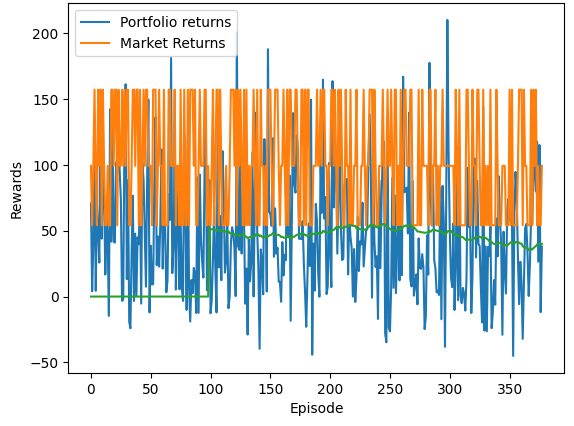
1000 days or roughly three years. The results show that it is not trivial to use a RL agent to trade on regular price data. The quality of the data, the changing
distribution of data, as well as the low signal to noise ratio makes it very difficult to ascertain any concrete patterns in the data. We can see that over time
as the model trains, the performance (portfolio returns over market) still remains very low.