Spectral clustering is a clustering algorithm which is often used in graph theory to separate nodes into distinct groups.
It does this in three main steps. Firstly, we extract an adjacency matrix from the graph. There are different ways of constructing this
matrix, but the underlying ideas remain the same. The adjacency matrix, as the name suggests, describes which nodes are "neighbouring" or
in close proximity to each other. This can be done in a discrete (nearest neighbours) or a more continuous way (using a RBF kernel). Using
this matrix, we can construct a graph Laplacian matrix. The Laplacian matrix of a graph describes many of its important properties, e.g. the sparsest
cut of the graph is approximated by the Fielder vector, which corresponds to the eigenvector related with the second smallest eigenvalue.
Second, we find the spectral decomposition (eigen decomposition) of the Laplacian matrix to retrieve the eigenvalues (spectrum) and corresponding eigenvectors. The eigenvectors are termed spectral
embeddings, which are often used reduced dimension embeddings of the original points. These eigenvectors also have a physical meaning - if we imagine the Laplacian matrix as a
"transformation" of the basis vectors, then the eigenvectors represent certain unit vectors on the space which are not "knocked" off their span. In other words,
eigenvectors are only multiplied by a constant factor when the Laplacian matrix is applied to them. Most choices of adjacency matrix result in symmetric Laplacian
matrices, so the resulting eigenvectors also form a new basis.
Finally, using these spectral embeddings, we can divide up the original points into a specified number of clusters, k. The most common method is to use
the K-means algorithm on the embeddings.
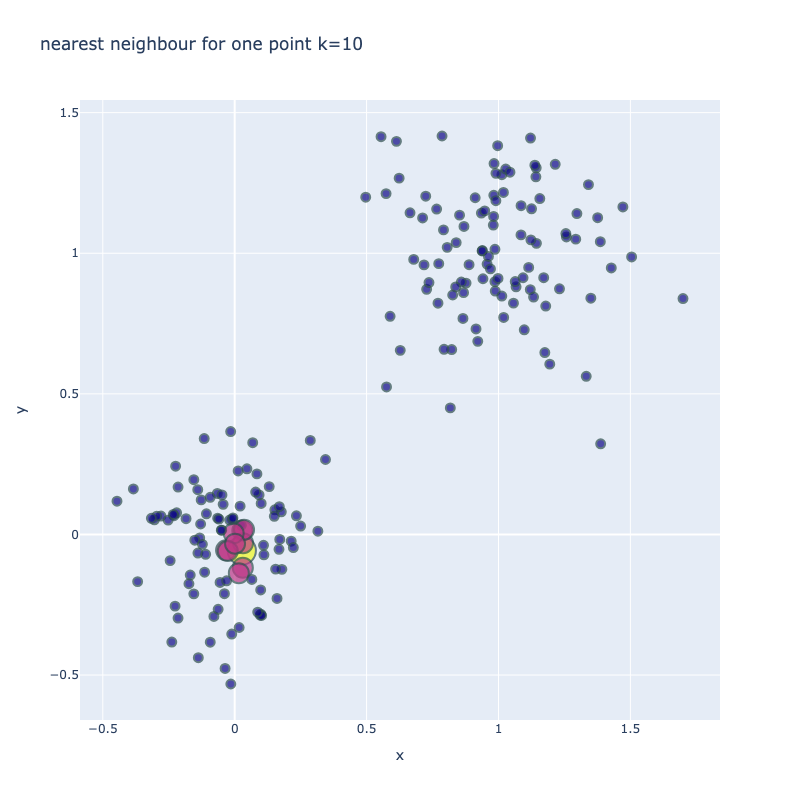
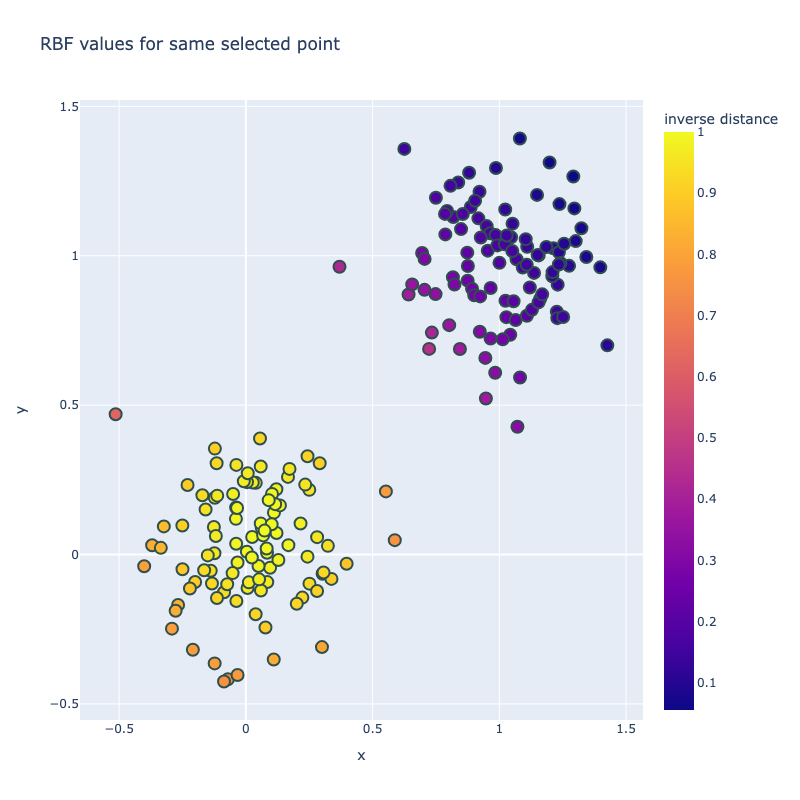
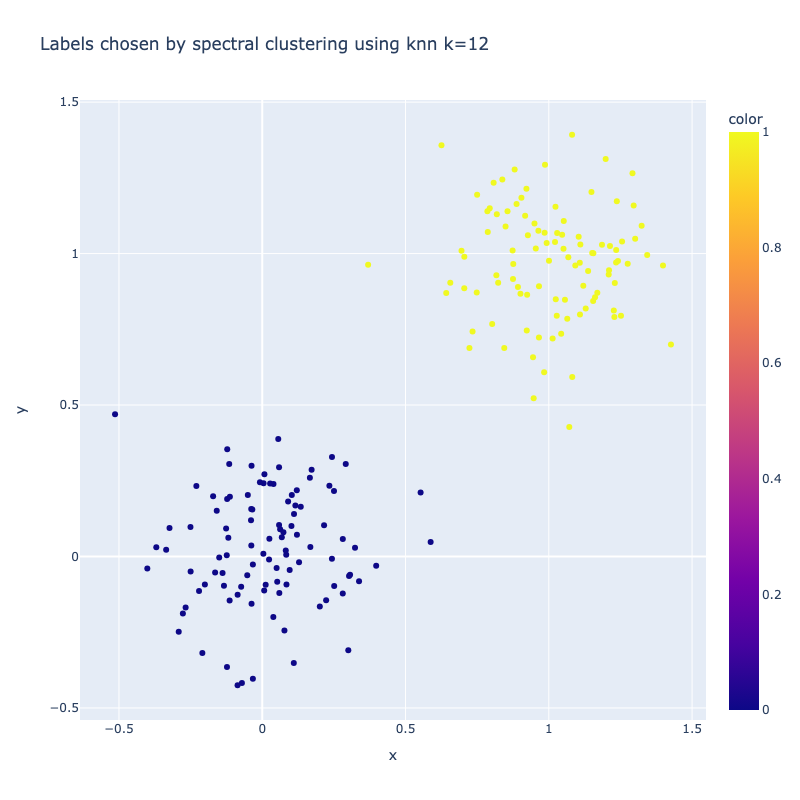
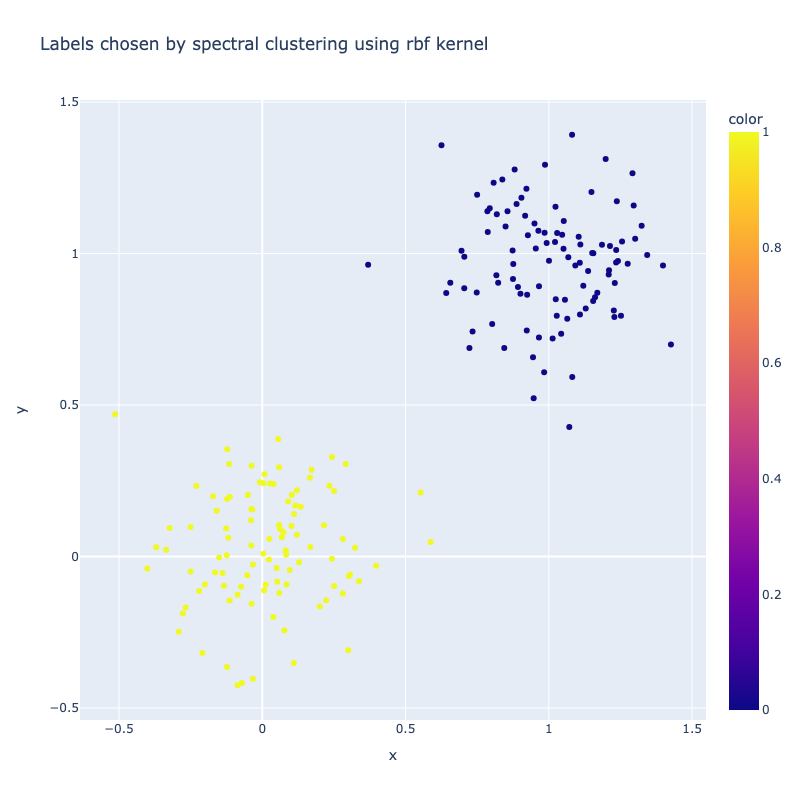
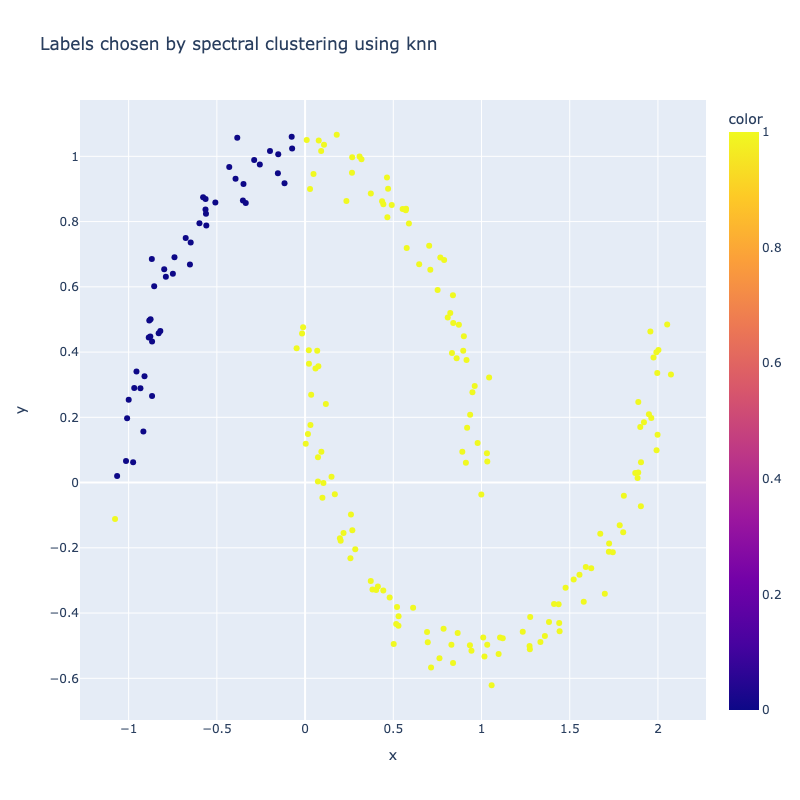
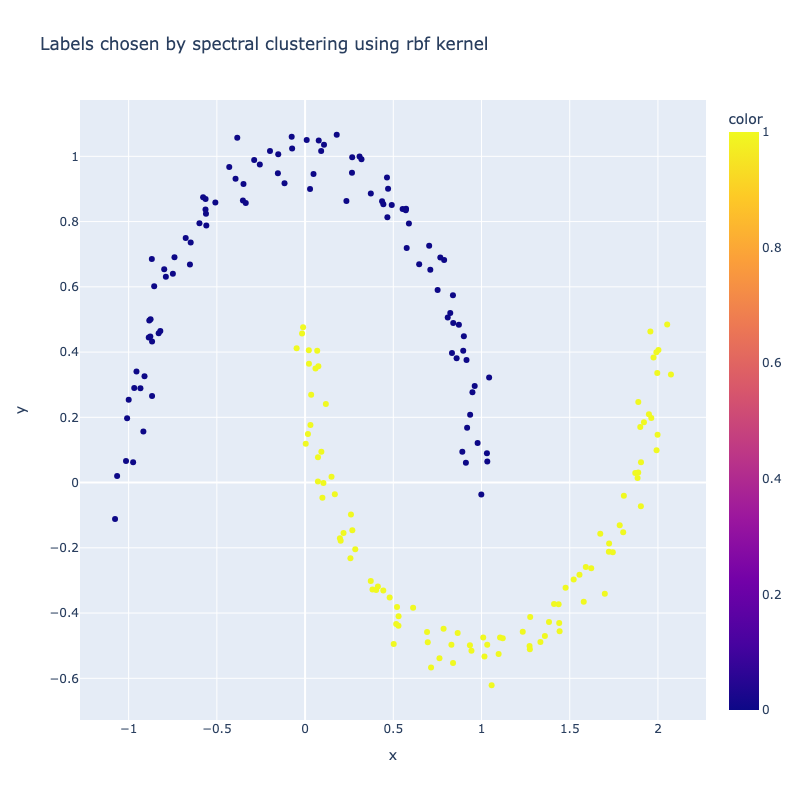
I implemented a spectral clustering algorithm using only numpy and the K-means function from sklearn. I trialled the two adjacency matrix mentioned above, on a simple problem, then a harder one to compare their performance. Both adjacency matrix methods are quite sensitive to hyperparameter values. The tuning process has been abstracted away, using a qualitative trial and error to find a value which classifies the most nodes correctly. Below are the results. It can be seen that the RBF kernel provides an advantage over the nearest neighbours approach, which misclassfies half of one crescent in the harder two moons problem, which is erroneously assigned to the wrong class due to its proximity to the tip of the other crescent. This is unsurprising, as by using nearest neighbours, we are essentially dropping important information about the n - k other nodes.